|
1990 Pattern Recognition and Image Processing Group 2021 2021- Virtual & Augmented Reality |

|
Curve and Fuzzy Curve Pyramids
 |
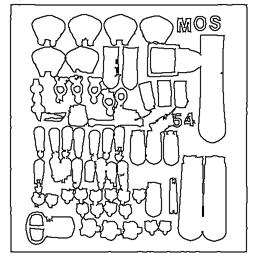 |
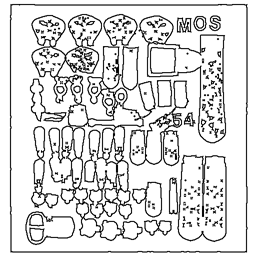
The curve pyramid where linear structures of images are represented by curve relations is shown. The basic steps for deriving a lower resolution representation of the curve pyramid and the properties of the 2x2/2 curve pyramid are described. As example, the 2x2/2 curve pyramid is used to remove short edge features of an edge image of archeological findings. Furthermore, the fuzzy curve pyramid as an extension of binary curve pyramids to curves with strenghts is demonstrated. Again, the basic steps for deriving a lower resolution representation and the properties are described. The fuzzy curve pyramid is applied to the same data of an edge image of archeological findings as the curve pyramid.
The 2 x 2 / 2 Curve Pyramid
The basic idea is to represent linear structures within images by curve relation. A cell of the underlying square grid is considered as the observation window through which the curve is observed. Consequently, only the intersection of the observed curve with the observation window is stored.
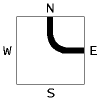
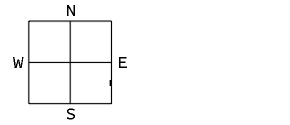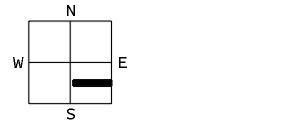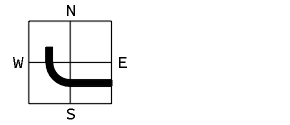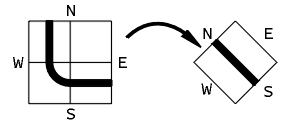
A NE curve relation
Curve relations are denoted by AB, where AB in (N=north, E=east, S=south, W=west, F) and F is a special end code when a curve ends within a cell.
The basic steps for deriving a lower resolution representation of the curve pyramid:
- split - subdivision of the cell contents by introducing a diagonal
- transitive closure - the curve relations of the four son cells are merged by computing the transitive closure of all relations
- reduce - the curve relations of the four diagonal elements of the new cell are selected
Reduction in the 2 x 2 / 2 curve pyramid.
Properties of the 2 x 2 / 2 curve pyramid
- a curve remains connected until it is completely covered by one cell. Then it disappears.
- length reduction property - short curves will disappear after a few levels and only long curves will be represented in higher levels of the pyramid. This property is used for structural noise filtering. First, the curve pyramid is built up to a certain level and afterwards all curves which are not present at this level are removed from the levels below.
2 x 2 / 2 Curve Pyramid Example
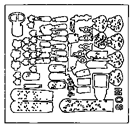
In this example, the 2x2/2 curve pyramid is used to remove short edge features of an edge image of archeological findings.
 Short image features (red) disappear according to the length reduction property:
Short image features (red) disappear according to the length reduction property:
The Seven Levels of the 2x2/2 Curve Pyramid in Detail
| Original Image | Curve Pyr. Level | Reduced Image |
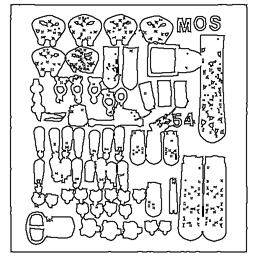 |
0 | 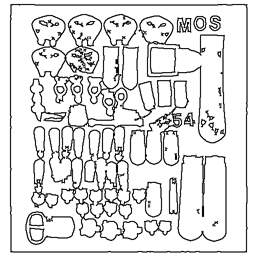 |
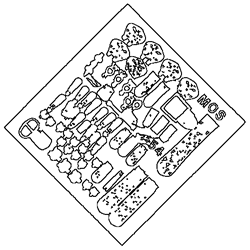 |
1 | 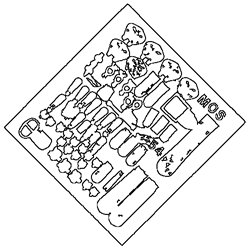 |
 |
2 | 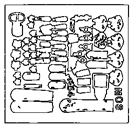 |
 |
3 |  |
 |
4 |  |
 |
5 |  |
 |
6 |  |
The 2 x 2 / 2 Fuzzy Curve Pyramid
Similar to the 2x2/2 curve pyramid, there are three step when constructing a fuzzy curve pyramid. Additionally, fuzzy criteria are introduced:
- fuzzy split - subdivision of the cell contents by introducing a diagonale.
- fuzzy transitive closure - construction of the curve relation of a cell at level n+1 out of the four triangles of level n.
- fuzzy reduce - the relation code used for processing the fuzzy transitive closure is converted to the code used by the next level.

Construction of a fuzzy curve pyramid
Properties of the 2 x 2 / 2 fuzzy curve pyramid:
- length reduction property - reduction of the number of curve code elements after every reduction step (similar to the 2x2/2 curve pyramid).
- minimum strength - if a single curve intersects the receptive field of a cell at level n, the grade-membership of the relation at level n will be the minimum of the grade-memberships of the curve segments of the base level.
- maximum strength - every curve will remain connected by the fuzzy reduction process and the strength of all fuzzy curve relations derived from one curve will be greater or equal to the strength of the curve in the base of the pyramid, i.e. the strength of the curve is preserved.
- minimax principle - the strength of a curve is the minimum of the strength of its segments. Furthermore, the strength of a side of a cell in the curve pyramid has the maximum strength of all curves intersecting this side.
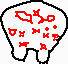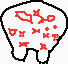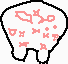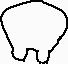
2 x 2 / 2 Fuzzy Curve Pyramid Example
In this example, the 2x2/2 fuzzy curve pyramid is used to remove short edge features of an edge image of archaeological findings
 Short image features (red) disappear according to the length reduction property:
Short image features (red) disappear according to the length reduction property:
The Seven Levels of the 2x2/2 Fuzzy Curve Pyramid in Detail
| Original Image | Fuzzy Curve Pyr. Level | Reduced Image |
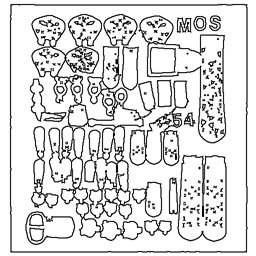 |
0 | 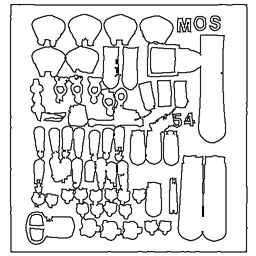 |
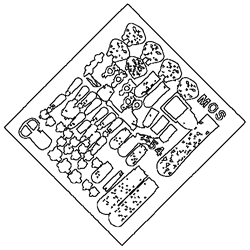 |
1 | 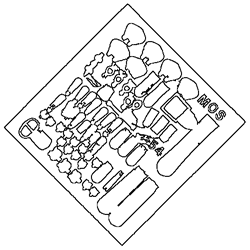 |
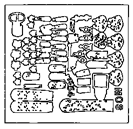 |
2 | 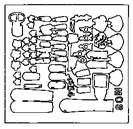 |
 |
3 |  |
 |
4 | 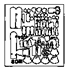 |
 |
5 |  |
 |
6 |  |
2014-2020 PRIP, Impressum / Datenschutzerklärung
This page is maintained by Webmaster ( webmaster(at)prip.tuwien.ac.at ) and was last modified on 18. March 2015 15:36